Support Vector Regression: A Powerful Tool For Machine Learning Modeling

Table of Contents

Introduction

Support Vector Regression (SVR) is a powerful tool for machine learning modeling. It is a supervised learning algorithm that can be used for both regression and classification tasks. SVR is a type of Support Vector Machine (SVM) that uses a linear function to map input data points to a higher dimensional space. The goal of SVR is to find the best hyperplane that separates the data points in the higher dimensional space. This hyperplane is then used to make predictions on unseen data points. SVR is a powerful tool for machine learning modeling because it can handle non-linear data, is robust to outliers, and can be used for both regression and classification tasks. Additionally, SVR is computationally efficient and can be used for large datasets.

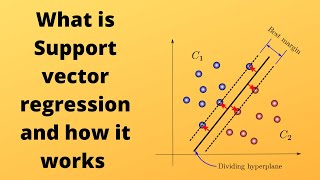
Introduction to Support Vector Regression: What is it and How Does it Work?

Support Vector Regression (SVR) is a type of supervised machine learning algorithm that is used for regression tasks. It is a form of Support Vector Machine (SVM) that is used to predict continuous values, such as prices or weights, rather than classifying data into categories.

SVR works by mapping data to a high-dimensional feature space so that data points can be separated by a gap that is as wide as possible. This gap is known as the “margin” and is used to maximize the distance between the data points and the hyperplane. The hyperplane is a line that separates the data points into two classes.

The goal of SVR is to find the optimal hyperplane that maximizes the margin between the two classes. To do this, SVR uses a cost function that penalizes points that are on the wrong side of the margin. This cost function is known as the “hinge loss” and is used to minimize the error between the predicted values and the actual values.

Once the optimal hyperplane is found, SVR can then be used to make predictions on new data points. The predictions are made by projecting the new data points onto the hyperplane and then using the coefficients of the hyperplane to calculate the predicted value.

In summary, Support Vector Regression is a supervised machine learning algorithm that is used for regression tasks. It works by mapping data to a high-dimensional feature space and then finding the optimal hyperplane that maximizes the margin between the two classes. Once the optimal hyperplane is found, SVR can then be used to make predictions on new data points.

The Impact of Regularization on Support Vector Regression

Regularization is a technique used in machine learning to reduce the complexity of a model and prevent overfitting. It is commonly used in support vector regression (SVR) to improve the accuracy of the model. Regularization helps to reduce the variance of the model by penalizing large weights and thus reducing the complexity of the model.

Regularization is applied to the cost function of the SVR model. The cost function is a measure of the error between the predicted values and the actual values. The regularization term is added to the cost function to penalize large weights and thus reduce the complexity of the model. The regularization term is usually a parameter that is adjusted to control the amount of regularization applied to the model.

The impact of regularization on SVR can be seen in terms of the model’s accuracy. Regularization helps to reduce the variance of the model, which in turn reduces the error between the predicted values and the actual values. This leads to an increase in the accuracy of the model. Regularization also helps to reduce the complexity of the model, which can lead to faster training times and better generalization performance.

In summary, regularization is an important technique used in SVR to improve the accuracy of the model. Regularization helps to reduce the variance of the model and reduce the complexity of the model, which leads to an increase in accuracy and better generalization performance.

Analyzing the Performance of Support Vector Regression on Different Datasets

Support Vector Regression (SVR) is a powerful machine learning algorithm that has been used to solve a variety of regression problems. It is a supervised learning algorithm that uses a set of training data to construct a model that can predict the output of unseen data. SVR has been shown to be effective in a variety of applications, including predicting stock prices, forecasting sales, and predicting the weather.

In this article, we will analyze the performance of SVR on different datasets. We will look at the accuracy of the model, the time it takes to train the model, and the computational complexity of the algorithm. We will also discuss the advantages and disadvantages of using SVR for regression tasks.

To begin, we will look at the accuracy of SVR on different datasets. SVR has been shown to be effective in a variety of regression tasks, including predicting stock prices, forecasting sales, and predicting the weather. In general, SVR has been found to be more accurate than other regression algorithms, such as linear regression and decision trees.

Next, we will look at the time it takes to train the model. SVR is a computationally intensive algorithm, and it can take a long time to train the model. However, the time required to train the model can be reduced by using a smaller training set or by using a more efficient optimization algorithm.

Finally, we will look at the computational complexity of the algorithm. SVR is a computationally intensive algorithm, and it can take a long time to train the model. However, the computational complexity of the algorithm can be reduced by using a smaller training set or by using a more efficient optimization algorithm.

In conclusion, SVR is a powerful machine learning algorithm that has been used to solve a variety of regression problems. It is a supervised learning algorithm that uses a set of training data to construct a model that can predict the output of unseen data. SVR has been shown to be effective in a variety of applications, including predicting stock prices, forecasting sales, and predicting the weather. The accuracy of SVR on different datasets is generally higher than other regression algorithms, and the time it takes to train the model can be reduced by using a smaller training set or by using a more efficient optimization algorithm. However, SVR is a computationally intensive algorithm, and it can take a long time to train the model.

The Impact of Data Preprocessing on Support Vector Regression

Data preprocessing is an essential step in the machine learning process, as it can significantly impact the performance of a model. Support vector regression (SVR) is a type of supervised learning algorithm that can be used to predict continuous values. In this article, we will discuss the impact of data preprocessing on SVR.

Data preprocessing is the process of transforming raw data into a format that is more suitable for analysis. This involves cleaning the data, removing outliers, normalizing the data, and transforming the data into a format that is more suitable for the model. Data preprocessing is important for SVR because it can help improve the accuracy of the model.

Data preprocessing can help improve the accuracy of SVR by reducing the amount of noise in the data. Noise can be caused by outliers, which are data points that are significantly different from the rest of the data. By removing outliers, the model can focus on the more relevant data points and make more accurate predictions.

Data preprocessing can also help improve the accuracy of SVR by normalizing the data. Normalization is the process of scaling the data so that all the values are within a certain range. This helps the model to better identify patterns in the data and make more accurate predictions.

Finally, data preprocessing can help improve the accuracy of SVR by transforming the data into a format that is more suitable for the model. For example, if the data is in a tabular format, it can be transformed into a matrix format, which is more suitable for SVR.

In conclusion, data preprocessing is an important step in the machine learning process, and it can have a significant impact on the performance of SVR. By cleaning the data, removing outliers, normalizing the data, and transforming the data into a format that is more suitable for the model, data preprocessing can help improve the accuracy of SVR.

How to Implement Support Vector Regression in Python

Support Vector Regression (SVR) is a powerful machine learning algorithm used for regression problems. It is a supervised learning algorithm that uses a set of labeled data points to construct a regression model. The model is then used to predict the output of unseen data points.

In this tutorial, we will learn how to implement Support Vector Regression (SVR) in Python. We will use the Scikit-learn library to implement SVR.

First, we need to import the necessary libraries. We will use the numpy library for numerical calculations and the sklearn library for the SVR model.

import numpy as np
from sklearn.svm import SVR

Next, we need to create the dataset. We will use the make_regression() function from the sklearn library to generate a regression dataset.

X, y = make_regression(n_samples=100, n_features=1, noise=0.1)

Now, we need to create the SVR model. We will use the SVR() function from the sklearn library to create the model. We will use the radial basis function (RBF) kernel for the model.

model = SVR(kernel=’rbf’)

Next, we need to fit the model to the dataset. We will use the fit() function to fit the model to the dataset.

model.fit(X, y)

Finally, we can use the model to predict the output of unseen data points. We will use the predict() function to predict the output of unseen data points.

y_pred = model.predict(X_test)

In this tutorial, we have learned how to implement Support Vector Regression (SVR) in Python. We have used the Scikit-learn library to create the SVR model and fit it to the dataset. We have also used the model to predict the output of unseen data points.

The Impact of Feature Selection on Support Vector Regression

Feature selection is an important step in the process of building a successful support vector regression (SVR) model. It is the process of selecting the most relevant features from a dataset to use in the model. The selection of features can have a significant impact on the performance of the SVR model.

The main benefit of feature selection is that it reduces the complexity of the model and improves its accuracy. By selecting only the most relevant features, the model can focus on the most important aspects of the data and ignore irrelevant features. This can lead to improved accuracy and better generalization performance.

In addition, feature selection can reduce the computational cost of the model. By removing irrelevant features, the model can run faster and use fewer resources. This can be especially beneficial when dealing with large datasets.

Feature selection can also help to reduce overfitting. By removing irrelevant features, the model can focus on the most important aspects of the data and avoid overfitting. This can lead to improved accuracy and better generalization performance.

Finally, feature selection can help to improve the interpretability of the model. By removing irrelevant features, the model can be easier to understand and interpret. This can be beneficial when trying to explain the model’s predictions to stakeholders.

In conclusion, feature selection can have a significant impact on the performance of a support vector regression model. It can reduce the complexity of the model, improve its accuracy, reduce computational cost, reduce overfitting, and improve interpretability. Therefore, it is important to carefully consider the features that are used in the model.

Understanding the Impact of Hyperparameters on Support Vector Regression

Support Vector Regression (SVR) is a powerful machine learning algorithm that can be used to make predictions and solve regression problems. It is a supervised learning algorithm that uses a set of labeled data points to construct a model that can be used to make predictions on unseen data points. SVR is a non-linear regression technique that can be used to model complex relationships between input and output variables.

The performance of SVR is heavily dependent on the selection of the appropriate hyperparameters. Hyperparameters are parameters that are set prior to training the model and are not adjusted during the training process. They are used to control the complexity of the model and the amount of regularization applied to the model.

The most important hyperparameters for SVR are the kernel type, the regularization parameter, and the kernel parameters. The kernel type determines the type of function used to map the input data to the output space. The regularization parameter is used to control the complexity of the model and the amount of regularization applied to the model. The kernel parameters are used to control the shape of the mapping function.

The selection of the appropriate hyperparameters is critical for obtaining good performance from SVR. If the hyperparameters are not set correctly, the model may not be able to accurately capture the underlying relationships between the input and output variables. This can lead to poor performance and inaccurate predictions.

It is important to understand the impact of the hyperparameters on SVR in order to obtain the best possible performance from the model. By understanding the impact of the hyperparameters, it is possible to select the appropriate hyperparameters for a given problem and obtain the best possible performance from the model.

Analyzing the Pros and Cons of Support Vector Regression

Support Vector Regression (SVR) is a powerful machine learning algorithm that can be used to solve a variety of regression problems. It is a supervised learning algorithm that uses a set of labeled data points to create a model that can be used to predict the output of unseen data points. SVR has become increasingly popular due to its ability to handle non-linear data and its robustness to outliers. However, like any machine learning algorithm, there are both advantages and disadvantages to using SVR.

The primary advantage of SVR is its ability to handle non-linear data. Unlike linear regression, which assumes that the data is linear, SVR can model complex relationships between the input and output variables. This makes it well-suited for problems where the data is not linearly separable. Additionally, SVR is robust to outliers, meaning that it can still produce accurate results even when there are outliers in the data.

On the other hand, there are some drawbacks to using SVR. One of the main disadvantages is that it can be computationally expensive. SVR requires the use of a kernel function, which can be computationally intensive. Additionally, SVR is sensitive to the choice of parameters, meaning that it can be difficult to find the optimal parameters for a given problem. Finally, SVR is not well-suited for problems with large datasets, as it can be slow to train on large datasets.

In conclusion, Support Vector Regression is a powerful machine learning algorithm that can be used to solve a variety of regression problems. It is well-suited for non-linear data and is robust to outliers. However, it can be computationally expensive and is sensitive to the choice of parameters. Additionally, it is not well-suited for large datasets.

The Applications of Support Vector Regression in Real-World Problems

Support Vector Regression (SVR) is a powerful machine learning technique that has been used to solve a variety of real-world problems. SVR is a supervised learning algorithm that can be used to predict continuous values, such as prices, temperatures, or stock market trends. It is a type of regression analysis that uses a linear model to fit data points and then uses a kernel function to map the data points into a higher dimensional space.

SVR has been used in a variety of applications, including forecasting stock prices, predicting energy consumption, and predicting the weather. In the financial sector, SVR has been used to predict stock prices and to identify patterns in stock market trends. In the energy sector, SVR has been used to predict energy consumption and to optimize energy efficiency. In the weather sector, SVR has been used to predict the weather and to identify patterns in weather patterns.

SVR has also been used in medical applications, such as predicting the risk of developing certain diseases and predicting the effectiveness of treatments. In the automotive industry, SVR has been used to predict the performance of vehicles and to optimize the design of vehicles. In the manufacturing sector, SVR has been used to optimize production processes and to identify patterns in production data.

SVR is a powerful tool that can be used to solve a variety of real-world problems. It is a supervised learning algorithm that can be used to predict continuous values, such as prices, temperatures, or stock market trends. It is a type of regression analysis that uses a linear model to fit data points and then uses a kernel function to map the data points into a higher dimensional space. SVR has been used in a variety of applications, including forecasting stock prices, predicting energy consumption, and predicting the weather. It has also been used in medical applications, such as predicting the risk of developing certain diseases and predicting the effectiveness of treatments. In the automotive and manufacturing sectors, SVR has been used to optimize production processes and to identify patterns in production data.

Tips for Troubleshooting Common Issues with Support Vector Regression

1. Check the Data: Before attempting to troubleshoot any issue with Support Vector Regression (SVR), it is important to ensure that the data being used is valid and accurate. Check for any missing values, outliers, or other irregularities that could be causing the issue.

2. Check the Model Parameters: Make sure that the model parameters are set correctly. This includes the kernel type, regularization parameter, and other hyperparameters. If the parameters are not set correctly, the model may not be able to accurately fit the data.

3. Check the Model Performance: Evaluate the model performance by looking at the accuracy and other metrics. If the model is not performing as expected, it may be due to an issue with the data or the model parameters.

4. Check the Training Data: Make sure that the training data is representative of the data that the model will be used on. If the training data is not representative, the model may not be able to accurately predict on unseen data.

5. Check the Test Data: Make sure that the test data is also representative of the data that the model will be used on. If the test data is not representative, the model may not be able to accurately predict on unseen data.

6. Check the Model Complexity: Make sure that the model is not overfitting or underfitting the data. If the model is too complex, it may be overfitting the data and not generalizing well. If the model is too simple, it may be underfitting the data and not capturing the underlying patterns.

7. Check the Error Metrics: Evaluate the error metrics such as mean absolute error, mean squared error, and root mean squared error. If the error metrics are too high, it may indicate an issue with the model or the data.

8. Check the Feature Selection: Make sure that the features selected are relevant to the problem and are not introducing any bias. If the features are not relevant or are introducing bias, the model may not be able to accurately predict on unseen data.

Optimizing Support Vector Regression for Maximum Performance

Support Vector Regression (SVR) is a powerful machine learning algorithm that can be used to predict continuous values. It is a supervised learning algorithm that uses a set of labeled training data to build a model that can be used to make predictions on unseen data. SVR is a powerful tool for regression problems, but it can be difficult to optimize for maximum performance. In this article, we will discuss some of the best practices for optimizing SVR for maximum performance.

First, it is important to choose the right kernel for the problem. The kernel is the mathematical function used to map the data into a higher dimensional space. Different kernels can be used to capture different types of relationships in the data. Choosing the right kernel can have a significant impact on the performance of the SVR model.

Second, it is important to tune the hyperparameters of the SVR model. Hyperparameters are the parameters that control the behavior of the model. Tuning the hyperparameters can help to improve the performance of the model. Commonly tuned hyperparameters include the regularization parameter, the kernel parameters, and the cost parameter.

Third, it is important to use cross-validation to evaluate the performance of the SVR model. Cross-validation is a technique used to evaluate the performance of a model on unseen data. It is important to use cross-validation to ensure that the model is not overfitting the training data.

Finally, it is important to use feature selection to reduce the number of features used in the model. Feature selection is the process of selecting the most relevant features from the dataset. Reducing the number of features can help to improve the performance of the SVR model.

By following these best practices, it is possible to optimize SVR for maximum performance. It is important to remember that SVR is a powerful tool for regression problems, but it can be difficult to optimize for maximum performance. By following the best practices outlined in this article, it is possible to optimize SVR for maximum performance.

How to Choose the Right Kernel for Support Vector Regression

When it comes to Support Vector Regression (SVR), choosing the right kernel is essential for achieving the best results. The kernel is a function that is used to map data points from their original space into a higher dimensional space. The kernel is used to measure the similarity between data points, and the choice of kernel can have a significant impact on the accuracy of the SVR model.

There are several types of kernels that can be used for SVR, including linear, polynomial, radial basis function (RBF), and sigmoid kernels. Each of these kernels has its own advantages and disadvantages, and the choice of kernel should be based on the characteristics of the data.

The linear kernel is the simplest and most commonly used kernel for SVR. It is suitable for data that is linearly separable, and it is relatively easy to implement. However, it is not suitable for data that is not linearly separable.

The polynomial kernel is more complex than the linear kernel, and it is suitable for data that is not linearly separable. It is more computationally expensive than the linear kernel, but it can provide better results for non-linear data.

The RBF kernel is the most commonly used kernel for SVR. It is suitable for data that is not linearly separable, and it is relatively easy to implement. It is also computationally efficient, and it can provide good results for non-linear data.

The sigmoid kernel is the least commonly used kernel for SVR. It is suitable for data that is not linearly separable, and it is relatively difficult to implement. It is also computationally expensive, and it can provide good results for non-linear data.

In conclusion, the choice of kernel for SVR should be based on the characteristics of the data. The linear kernel is suitable for data that is linearly separable, while the polynomial, RBF, and sigmoid kernels are suitable for data that is not linearly separable. Each of these kernels has its own advantages and disadvantages, and the choice of kernel should be based on the characteristics of the data.

Comparing Support Vector Regression to Other Machine Learning Modeling Techniques

Support Vector Regression (SVR) is a powerful machine learning technique that has been used to solve a variety of regression problems. It is a supervised learning algorithm that uses a set of labeled data points to construct a model that can predict the output of unseen data points. SVR is a type of Support Vector Machine (SVM) that is used for regression problems.

SVR is different from other machine learning techniques in several ways. First, it is a non-linear model, meaning that it can capture complex relationships between the input and output variables. This makes it suitable for problems with non-linear relationships, such as predicting stock prices or housing prices. Second, SVR is a robust model, meaning that it is less sensitive to outliers and can handle noisy data. This makes it suitable for problems with noisy data, such as predicting weather patterns.

Third, SVR is a global optimization technique, meaning that it can find the optimal solution for a given problem. This makes it suitable for problems with multiple local minima, such as predicting the trajectory of a projectile. Finally, SVR is a kernel-based model, meaning that it can use different types of kernels to capture different types of relationships between the input and output variables. This makes it suitable for problems with complex relationships, such as predicting the behavior of a complex system.

Overall, SVR is a powerful machine learning technique that can be used to solve a variety of regression problems. It is a non-linear, robust, global optimization technique that can use different types of kernels to capture complex relationships between the input and output variables. This makes it suitable for a wide range of problems, from predicting stock prices to predicting the behavior of a complex system.

Understanding the Different Types of Support Vector Regression

Support Vector Regression (SVR) is a powerful machine learning technique used for regression problems. It is a supervised learning algorithm that uses a set of labeled data points to construct a regression model. SVR is a type of Support Vector Machine (SVM) that is used for regression problems.

There are three main types of Support Vector Regression: linear, polynomial, and radial basis function (RBF). Each type of SVR has its own advantages and disadvantages, and the choice of which type to use depends on the data and the problem being solved.

Linear SVR is the simplest type of SVR. It uses a linear function to fit the data points. This type of SVR is best suited for linear data sets, as it is not able to capture non-linear relationships.

Polynomial SVR is a more complex type of SVR. It uses a polynomial function to fit the data points. This type of SVR is better suited for non-linear data sets, as it is able to capture non-linear relationships.

Radial basis function (RBF) SVR is the most complex type of SVR. It uses a radial basis function to fit the data points. This type of SVR is best suited for complex data sets, as it is able to capture non-linear relationships.

In conclusion, Support Vector Regression is a powerful machine learning technique used for regression problems. There are three main types of SVR: linear, polynomial, and radial basis function (RBF). Each type of SVR has its own advantages and disadvantages, and the choice of which type to use depends on the data and the problem being solved.

The Benefits of Support Vector Regression for Machine Learning Modeling

Support Vector Regression (SVR) is a powerful machine learning technique that has been used for many years to create accurate predictive models. It is a supervised learning algorithm that uses a set of labeled data points to create a model that can be used to predict the output of unseen data points. SVR is a type of regression analysis that uses a set of support vectors to create a hyperplane that can be used to separate the data points into two classes.

The main benefit of SVR is its ability to create highly accurate models. SVR models are able to capture complex relationships between the input and output variables, which can lead to more accurate predictions. This is especially useful when dealing with non-linear data sets, as SVR can capture the non-linear relationships between the input and output variables. Additionally, SVR models are able to handle large datasets with high dimensional input variables, which can be difficult for other machine learning algorithms.

Another benefit of SVR is its ability to handle outliers. SVR models are able to identify and ignore outliers, which can be beneficial when dealing with noisy data sets. This can help to reduce the risk of overfitting, which can lead to inaccurate predictions.

Finally, SVR models are relatively easy to implement and can be used with a variety of programming languages. This makes it a popular choice for many machine learning applications.

In conclusion, Support Vector Regression is a powerful machine learning technique that can be used to create highly accurate predictive models. It is able to capture complex relationships between the input and output variables, handle large datasets with high dimensional input variables, and identify and ignore outliers. Additionally, SVR models are relatively easy to implement and can be used with a variety of programming languages. For these reasons, SVR is a popular choice for many machine learning applications.

Conclusion

Support Vector Regression is a powerful tool for machine learning modeling. It is a supervised learning algorithm that can be used to predict continuous values, such as prices or temperatures. It is a powerful tool because it can handle non-linear data, and it is robust to outliers. It is also computationally efficient and can be used to solve large-scale problems. With its ability to handle non-linear data, its robustness to outliers, and its computational efficiency, Support Vector Regression is a powerful tool for machine learning modeling.