Understanding The Applications Of Multiple Linear Regression In Machine Learning

Table of Contents

Introduction

Multiple linear regression is a powerful tool in machine learning that can be used to predict the outcome of a given set of data. It is a type of linear regression that uses multiple independent variables to predict the outcome of a dependent variable. It is a powerful tool for predicting the outcome of a given set of data and can be used to make decisions about how to best use the data. In this article, we will discuss the applications of multiple linear regression in machine learning and how it can be used to make better decisions. We will also discuss the advantages and disadvantages of using multiple linear regression in machine learning. Finally, we will discuss some of the best practices for using multiple linear regression in machine learning.

Comparing Multiple Linear Regression to Other Regression Techniques

Multiple linear regression is a powerful and widely used regression technique that is used to model the relationship between a dependent variable and two or more independent variables. It is a type of linear regression that is used when there are multiple independent variables that are related to the dependent variable. This technique is used to identify the strength of the relationship between the independent variables and the dependent variable.

Multiple linear regression is a powerful tool for predicting the value of a dependent variable based on the values of multiple independent variables. It is a useful technique for understanding the relationship between multiple independent variables and a single dependent variable. It can also be used to identify the most important independent variables that have the greatest impact on the dependent variable. Basics of Linear Regression for Machine Learning

Multiple linear regression is different from other regression techniques in that it is used to model the relationship between multiple independent variables and a single dependent variable. Other regression techniques, such as logistic regression, are used to model the relationship between a single independent variable and a single dependent variable. Additionally, multiple linear regression is used to identify the strength of the relationship between the independent variables and the dependent variable, while other regression techniques are used to identify the probability of an outcome based on the values of the independent variables.

Overall, multiple linear regression is a powerful and widely used regression technique that is used to model the relationship between a dependent variable and two or more independent variables. It is a useful tool for understanding the relationship between multiple independent variables and a single dependent variable, and for identifying the most important independent variables that have the greatest impact on the dependent variable. It is different from other regression techniques in that it is used to model the relationship between multiple independent variables and a single dependent variable, and to identify the strength of the relationship between the independent variables and the dependent variable.

The Basics of Multiple Linear Regression in Machine Learning

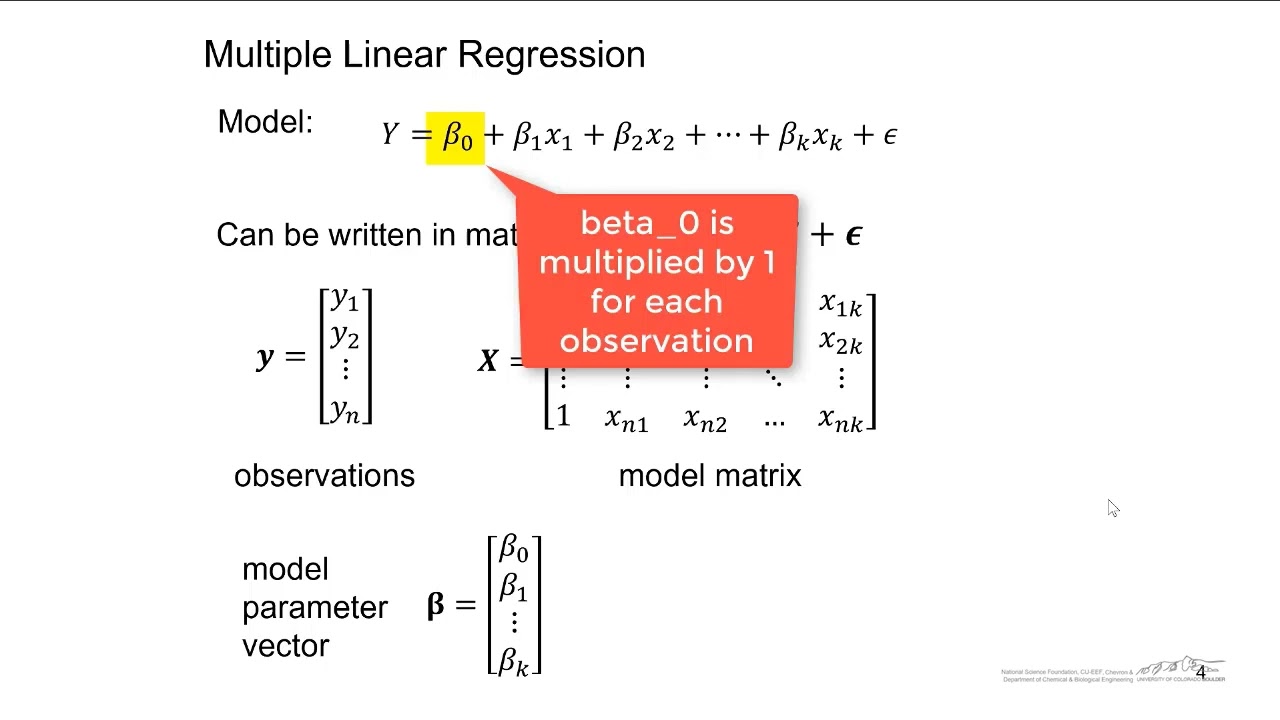
Multiple linear regression is a powerful machine learning technique used to predict a continuous outcome variable from a set of predictor variables. It is a supervised learning algorithm that assumes a linear relationship between the predictor variables and the outcome variable.

Multiple linear regression is a linear regression model that uses multiple predictor variables to predict the outcome variable. It is a statistical technique that uses multiple independent variables to predict the value of a dependent variable. The independent variables are also known as predictors, regressors, or features, while the dependent variable is also known as the response or target variable.

The multiple linear regression model is expressed as a linear equation, where the coefficients of the independent variables are estimated using the least squares method. The coefficients are estimated by minimizing the sum of the squared errors between the observed values and the predicted values. The model is then used to make predictions about the dependent variable based on the values of the independent variables.

Multiple linear regression can be used to identify the relationships between the predictor variables and the outcome variable. It can also be used to identify the most important predictor variables and to identify the most influential predictor variables.

Multiple linear regression can be used to identify the effects of different predictor variables on the outcome variable. It can also be used to identify the most important predictor variables and to identify the most influential predictor variables.

Multiple linear regression is a powerful machine learning technique that can be used to identify the relationships between predictor variables and the outcome variable. It can also be used to identify the most important predictor variables and to identify the most influential predictor variables.

The Benefits of Automated Feature Selection for Multiple Linear Regression

Automated feature selection is a powerful tool for multiple linear regression, as it can help to reduce the complexity of the model and improve its accuracy. Automated feature selection is a process of selecting the most relevant features from a dataset to be used in a model. This process can be used to reduce the number of features in a dataset, which can help to reduce the complexity of the model and improve its accuracy.

The main benefit of automated feature selection is that it can help to reduce the number of features in a dataset, which can help to reduce the complexity of the model and improve its accuracy. By reducing the number of features, the model can be more easily understood and interpreted. Additionally, automated feature selection can help to reduce the risk of overfitting, as it can help to identify and remove features that are not relevant to the model.

Another benefit of automated feature selection is that it can help to reduce the computational cost of the model. By reducing the number of features, the model can be more efficiently trained and evaluated. Additionally, automated feature selection can help to reduce the risk of overfitting, as it can help to identify and remove features that are not relevant to the model.

Finally, automated feature selection can help to improve the interpretability of the model. By reducing the number of features, the model can be more easily understood and interpreted. Additionally, automated feature selection can help to identify and remove features that are not relevant to the model, which can help to improve the accuracy of the model.

In conclusion, automated feature selection is a powerful tool for multiple linear regression, as it can help to reduce the complexity of the model and improve its accuracy. Automated feature selection can help to reduce the number of features in a dataset, reduce the computational cost of the model, and improve the interpretability of the model.

Understanding the Role of Feature Engineering in Multiple Linear Regression

Feature engineering is an important step in the process of multiple linear regression. It is the process of transforming raw data into features that better represent the underlying problem and allow for better predictive models. Feature engineering can help to improve the accuracy of a model by creating new features that capture more information about the data.

Feature engineering involves selecting, creating, and transforming features that are relevant to the problem at hand. This process can involve a variety of techniques, such as feature selection, feature extraction, and feature transformation. Feature selection involves selecting the most relevant features from the dataset. Feature extraction involves creating new features from existing features. Feature transformation involves transforming existing features into new ones.

Feature engineering can help to improve the accuracy of a multiple linear regression model by creating new features that capture more information about the data. For example, if a dataset contains a large number of features, feature engineering can help to reduce the number of features by selecting the most relevant ones. This can help to reduce the complexity of the model and improve its accuracy. Additionally, feature engineering can help to create new features that capture more information about the data, which can help to improve the accuracy of the model.

In summary, feature engineering is an important step in the process of multiple linear regression. It involves selecting, creating, and transforming features that are relevant to the problem at hand. Feature engineering can help to improve the accuracy of a model by creating new features that capture more information about the data.

Analyzing the Impact of Data Preprocessing on Multiple Linear Regression

Data preprocessing is an essential step in the development of a successful multiple linear regression model. It involves the transformation of raw data into a format that is suitable for further analysis. Preprocessing can have a significant impact on the accuracy and performance of the model, and it is important to understand the implications of preprocessing on the model.

Data preprocessing can be divided into two main categories: feature engineering and data cleaning. Feature engineering involves the selection and transformation of features to improve the accuracy of the model. This includes the selection of relevant features, the transformation of features to improve their predictive power, and the creation of new features from existing ones. Data cleaning involves the removal of outliers, missing values, and other irregularities in the data.

The impact of data preprocessing on multiple linear regression can be seen in several ways. First, preprocessing can improve the accuracy of the model by selecting and transforming features that are more predictive of the target variable. This can lead to better model performance and more accurate predictions. Second, preprocessing can reduce the complexity of the model by removing irrelevant features and reducing the number of features used in the model. This can lead to faster training times and improved model performance. Finally, preprocessing can reduce the risk of overfitting by removing outliers and other irregularities in the data.

In conclusion, data preprocessing is an important step in the development of a successful multiple linear regression model. It can improve the accuracy of the model by selecting and transforming features, reduce the complexity of the model, and reduce the risk of overfitting. Therefore, it is important to understand the implications of preprocessing on the model and ensure that it is done correctly.

The Applications of Multiple Linear Regression in Business

Multiple linear regression is a powerful tool used in business to analyze the relationship between multiple independent variables and a single dependent variable. It is a statistical technique that can be used to identify the impact of multiple independent variables on a single dependent variable. This technique is widely used in business to understand the relationship between different factors and the outcome of a particular business decision.

Multiple linear regression can be used to identify the impact of different factors on the sales of a product. For example, a business can use multiple linear regression to identify the impact of different marketing strategies, such as advertising, promotions, and pricing, on the sales of a product. This technique can also be used to identify the impact of different economic factors, such as inflation, interest rates, and exchange rates, on the sales of a product.

Multiple linear regression can also be used to identify the impact of different factors on the profitability of a business. For example, a business can use multiple linear regression to identify the impact of different cost factors, such as labor costs, raw material costs, and overhead costs, on the profitability of the business. This technique can also be used to identify the impact of different economic factors, such as inflation, interest rates, and exchange rates, on the profitability of the business.

Multiple linear regression can also be used to identify the impact of different factors on the stock price of a company. For example, a business can use multiple linear regression to identify the impact of different economic factors, such as inflation, interest rates, and exchange rates, on the stock price of a company. This technique can also be used to identify the impact of different corporate actions, such as mergers and acquisitions, on the stock price of a company.

Overall, multiple linear regression is a powerful tool used in business to analyze the relationship between multiple independent variables and a single dependent variable. It can be used to identify the impact of different factors on the sales, profitability, and stock price of a business. This technique is widely used in business to understand the relationship between different factors and the outcome of a particular business decision.

Using Multiple Linear Regression to Solve Real-World Problems

Multiple linear regression is a powerful tool used to solve real-world problems. It is a statistical technique used to predict the value of a dependent variable based on the values of two or more independent variables. This technique is used in a variety of fields, including economics, finance, marketing, and engineering.

In economics, multiple linear regression is used to analyze the relationship between economic variables such as GDP, inflation, and unemployment. By using this technique, economists can identify the factors that influence economic growth and make predictions about future economic trends.

In finance, multiple linear regression is used to analyze the relationship between stock prices and other factors such as earnings, dividends, and interest rates. By using this technique, investors can identify the factors that influence stock prices and make informed decisions about their investments.

In marketing, multiple linear regression is used to analyze the relationship between customer behavior and other factors such as demographics, product features, and advertising. By using this technique, marketers can identify the factors that influence customer behavior and develop effective marketing strategies.

In engineering, multiple linear regression is used to analyze the relationship between physical properties and other factors such as temperature, pressure, and humidity. By using this technique, engineers can identify the factors that influence the performance of a product and develop better designs.

Multiple linear regression is a powerful tool used to solve real-world problems. It is used in a variety of fields to identify the factors that influence a particular outcome and make predictions about future trends. By using this technique, economists, investors, marketers, and engineers can gain valuable insights into their respective fields and make informed decisions.

The Role of Regularization in Multiple Linear Regression

Regularization is an important technique used in multiple linear regression to reduce the complexity of the model and prevent overfitting. It is a process of adding a penalty term to the objective function of the model in order to reduce the magnitude of the coefficients of the model. This helps to reduce the variance of the model and improve its generalization ability.

Regularization is used to reduce the complexity of the model by penalizing large coefficients. This is done by adding a penalty term to the objective function of the model. The penalty term is usually a function of the magnitude of the coefficients. The most commonly used penalty terms are the L1 and L2 regularization terms. The L1 regularization term penalizes the sum of the absolute values of the coefficients, while the L2 regularization term penalizes the sum of the squares of the coefficients.

Regularization helps to reduce the variance of the model by reducing the magnitude of the coefficients. This helps to improve the generalization ability of the model by reducing the chances of overfitting. Regularization also helps to reduce the complexity of the model by reducing the number of features that are used in the model. This helps to reduce the computational cost of the model and improve its performance.

In conclusion, regularization is an important technique used in multiple linear regression to reduce the complexity of the model and prevent overfitting. It helps to reduce the variance of the model and improve its generalization ability. Regularization also helps to reduce the number of features used in the model and reduce the computational cost of the model.

Understanding the Impact of Feature Selection on Multiple Linear Regression

Feature selection is an important step in the process of building a multiple linear regression model. It involves selecting a subset of features from a larger set of features that are most relevant to the model. The selection of features can have a significant impact on the performance of the model.

The primary goal of feature selection is to reduce the complexity of the model and improve its accuracy. By selecting only the most relevant features, the model can be simplified and the number of parameters can be reduced. This can lead to improved accuracy and better generalization of the model.

In addition, feature selection can also help to reduce the risk of overfitting. By selecting only the most relevant features, the model can be less prone to overfitting and can better generalize to unseen data. This can lead to improved accuracy and better performance on unseen data.

Finally, feature selection can also help to reduce the computational cost of the model. By selecting only the most relevant features, the model can be more efficient and require less computational resources. This can lead to improved performance and faster training times.

In summary, feature selection is an important step in the process of building a multiple linear regression model. It can help to reduce the complexity of the model, reduce the risk of overfitting, and reduce the computational cost of the model. All of these factors can lead to improved accuracy and better performance on unseen data.

Analyzing the Performance of Multiple Linear Regression Models

Multiple linear regression is a powerful tool for analyzing data and predicting outcomes. It is a type of regression analysis that uses multiple independent variables to predict a single dependent variable. This type of regression model can be used to identify relationships between variables, identify trends, and make predictions.

When analyzing the performance of multiple linear regression models, there are several factors to consider. First, the model should be evaluated for accuracy. This can be done by comparing the predicted values to the actual values. If the model is accurate, the predicted values should be close to the actual values.

Second, the model should be evaluated for its ability to explain the data. This can be done by looking at the R-squared value, which measures the amount of variation in the dependent variable that is explained by the independent variables. A higher R-squared value indicates that the model is better able to explain the data.

Third, the model should be evaluated for its ability to make predictions. This can be done by looking at the root mean squared error (RMSE), which measures the average difference between the predicted values and the actual values. A lower RMSE indicates that the model is better able to make accurate predictions.

Finally, the model should be evaluated for its ability to generalize to new data. This can be done by looking at the cross-validation score, which measures the model’s ability to make accurate predictions on unseen data. A higher cross-validation score indicates that the model is better able to generalize to new data.

By evaluating the performance of multiple linear regression models on these four criteria, it is possible to determine which model is best suited for a given task. This can help ensure that the model is able to accurately explain the data, make accurate predictions, and generalize to new data.

The Different Types of Multiple Linear Regression Models

Multiple linear regression is a statistical technique used to analyze the relationship between multiple independent variables and a single dependent variable. It is a powerful tool for predicting the value of the dependent variable based on the values of the independent variables. There are several different types of multiple linear regression models, each with its own advantages and disadvantages.

The first type of multiple linear regression model is the standard linear regression model. This model is used when all of the independent variables are continuous and the dependent variable is continuous. It is the most commonly used type of multiple linear regression model and is used to predict the value of the dependent variable based on the values of the independent variables.

The second type of multiple linear regression model is the logistic regression model. This model is used when the dependent variable is categorical and the independent variables are continuous. It is used to predict the probability of a certain outcome based on the values of the independent variables.

The third type of multiple linear regression model is the polynomial regression model. This model is used when the dependent variable is continuous and the independent variables are polynomials. It is used to predict the value of the dependent variable based on the values of the independent variables.

The fourth type of multiple linear regression model is the stepwise regression model. This model is used when the dependent variable is continuous and the independent variables are categorical. It is used to identify the most important independent variables that have the greatest impact on the dependent variable.

Finally, the fifth type of multiple linear regression model is the ridge regression model. This model is used when the dependent variable is continuous and the independent variables are correlated. It is used to reduce the variance of the model by penalizing the coefficients of the independent variables.

Each of these types of multiple linear regression models has its own advantages and disadvantages. It is important to understand the strengths and weaknesses of each model before deciding which one to use.

Comparing Multiple Linear Regression to Other Machine Learning Algorithms

Multiple linear regression is a powerful machine learning algorithm that is used to predict the value of a continuous target variable based on the values of multiple independent variables. It is a supervised learning algorithm, meaning that it requires labeled data in order to make predictions.

Multiple linear regression is a linear model, meaning that it assumes a linear relationship between the independent variables and the target variable. This makes it a relatively simple algorithm to understand and implement, and it is often used as a baseline model for comparison with more complex algorithms.

However, multiple linear regression has some limitations. It is not able to capture non-linear relationships between the independent variables and the target variable, and it is also not able to capture interactions between the independent variables. For these reasons, it is often not the best choice for more complex datasets.

In these cases, other machine learning algorithms may be more suitable. For example, decision trees are able to capture non-linear relationships and interactions between the independent variables, and they are also able to handle datasets with a large number of features. Support vector machines are also able to capture non-linear relationships, and they are often used for classification tasks. Neural networks are even more powerful, and they are able to capture complex relationships between the independent variables and the target variable.

In summary, multiple linear regression is a powerful and simple machine learning algorithm that is often used as a baseline model for comparison with more complex algorithms. However, it has some limitations, and for more complex datasets, other machine learning algorithms may be more suitable.

Understanding the Limitations of Multiple Linear Regression in Machine Learning

Multiple linear regression is a powerful tool for predicting outcomes in machine learning. It is a statistical technique that uses multiple independent variables to predict a single dependent variable. However, it is important to understand the limitations of this technique in order to use it effectively.

First, multiple linear regression assumes that the relationship between the independent and dependent variables is linear. This means that the relationship between the variables is not necessarily linear in reality. If the relationship is non-linear, the model will not be able to accurately predict the outcome.

Second, multiple linear regression assumes that there is no multicollinearity between the independent variables. Multicollinearity occurs when two or more independent variables are highly correlated with each other. This can lead to inaccurate predictions because the model will not be able to distinguish between the effects of the different variables.

Third, multiple linear regression assumes that there is no autocorrelation between the independent variables. Autocorrelation occurs when the value of one variable is correlated with the value of another variable at a different time. This can lead to inaccurate predictions because the model will not be able to distinguish between the effects of the different variables.

Finally, multiple linear regression assumes that the data is normally distributed. If the data is not normally distributed, the model will not be able to accurately predict the outcome.

In conclusion, multiple linear regression is a powerful tool for predicting outcomes in machine learning. However, it is important to understand the limitations of this technique in order to use it effectively. By understanding these limitations, you can ensure that your model is able to accurately predict the outcome.

The Benefits of Multiple Linear Regression in Machine Learning

Multiple linear regression is a powerful tool in machine learning that can be used to predict the value of a dependent variable based on the values of multiple independent variables. This type of regression is useful for analyzing complex relationships between variables and can be used to make predictions about future outcomes.

The primary benefit of multiple linear regression is its ability to identify relationships between multiple independent variables and a single dependent variable. By using multiple linear regression, researchers can identify which independent variables have the most influence on the dependent variable. This can be used to make predictions about future outcomes and to identify which variables are most important in determining the outcome.

Multiple linear regression also allows researchers to identify non-linear relationships between variables. This is important because many real-world relationships are non-linear and cannot be accurately modeled using traditional linear regression techniques. By using multiple linear regression, researchers can identify these non-linear relationships and use them to make more accurate predictions.

Another benefit of multiple linear regression is its ability to identify interactions between independent variables. This is important because many real-world relationships are not linear but are instead affected by interactions between multiple variables. By using multiple linear regression, researchers can identify these interactions and use them to make more accurate predictions.

Finally, multiple linear regression is a powerful tool for data analysis. By using multiple linear regression, researchers can identify relationships between variables, make predictions about future outcomes, and identify interactions between variables. This makes multiple linear regression a powerful tool for data analysis and can be used to gain insights into complex relationships between variables.

How to Use Multiple Linear Regression to Make Predictions in Machine Learning

Multiple linear regression is a powerful tool used in machine learning to make predictions. It is a type of supervised learning algorithm that uses multiple independent variables to predict a dependent variable. It is a linear approach to modeling the relationship between a dependent variable and one or more independent variables.

The basic idea behind multiple linear regression is to use multiple independent variables to predict a dependent variable. The independent variables are also known as predictors, and the dependent variable is the outcome or response. The model is built by finding the best fit line that minimizes the sum of the squared errors between the predicted and actual values.

To use multiple linear regression to make predictions in machine learning, the first step is to collect data. This data should include the independent variables and the dependent variable. The independent variables should be related to the dependent variable in some way. Once the data is collected, it should be split into training and testing sets. The training set is used to build the model, while the testing set is used to evaluate the model’s performance.

The next step is to build the model. This is done by using a linear regression algorithm to find the best fit line that minimizes the sum of the squared errors between the predicted and actual values. Once the model is built, it can be used to make predictions on new data.

Multiple linear regression can be used to make predictions in machine learning. It is a powerful tool that can be used to model the relationship between a dependent variable and one or more independent variables. By collecting data, splitting it into training and testing sets, and building a model, multiple linear regression can be used to make predictions in machine learning.

Conclusion

In conclusion, multiple linear regression is a powerful tool for machine learning that can be used to make predictions and analyze data. It is a versatile technique that can be used to solve a variety of problems, from predicting stock prices to predicting customer churn. With the right data and the right model, multiple linear regression can be used to make accurate predictions and provide valuable insights.